$M^x/M/1$ Queueing System
Compound Poisson arrival proccess(CPP)의 형태로 job이 도착하는데, 이를 다른 말로는 Batch 또는 Bulk arrival이라고 한다.
기존의 \(M/M/1\) 모델과의 차이점은, 한 번의 arrival에 여러개의 job이 들어올 수 있다는 점이다. 이것은 한 번의 arrival에 한 번의 job이 도착하는 여러개의 Poisson process의 합으로 볼 수 있다.
이 때 batch의 크기는 다음의 일반적인 분포를 따르는 random variable G라고 하자.
$$ Pr\{G = n\} = g_n \quad (n \geq 1)$$
시스템의 성능을 평가하기 위해서는 여러 지표들을 뽑아야 한다. 그 중 대표적으로 쓰는 것이 평균 job 수 \(\bar{N}\)이다. 그동안에는 \(\bar{N}\)을 구하기 위해서는 probability distribution \(Pr\{N(t)=n\}\)을 구했지만, 이제부터는 이것을 구하기 어렵다. 따라서 앞으로는 Probability Generating Function을 사용해서 \(\bar{N}\)을 구하게 된다.
우선 \(M^x/M/1\)의 state transition diagram을 그리면 아래와 같다.
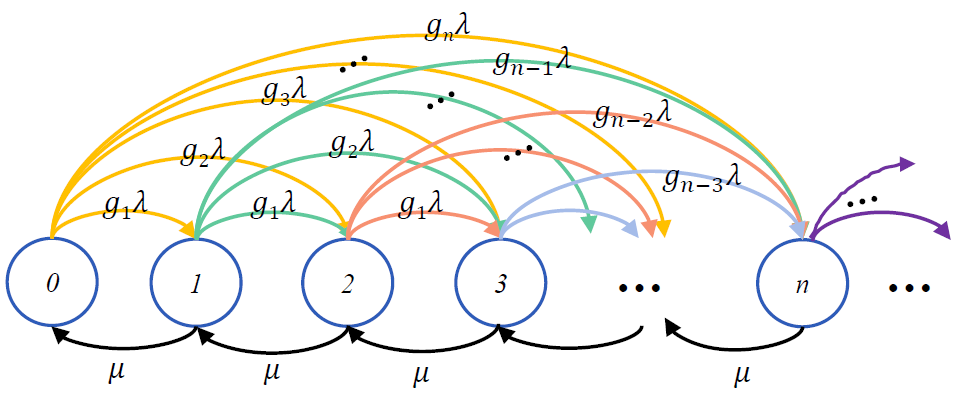
위 그림에서, 다음 식들을 유도할 수 있다.
$$\lambda P_0 = \mu P_1 \quad \cdots (1)$$
$$(\lambda + \mu)P_n = \mu P_{n+1} + \lambda \sum_{k=1}^n g_k P_{n-k} \quad (n \geq 1) \quad \cdots (2)$$
\(\bar{N}\)을 구하는 2가지 방법
-
\(n P_n\)을 가능한한 구해서 대략적인 값을 구하기
\(\bar{N} \approx \sum_{k=0}^n k P_k \quad (n Pn < \varepsilon)\)
-
Probability generating function에서 \(\bar{N}\) 구하기
state variable \(X\)에 대한 probability generating function \(Y(z) = E[z^X]\)에 대해서, \(E[X] = Y'(1)\)
\(\bar{N}\) 계산하기
state variable \(X\)에 대한 probability generating function \(Y(z)\)에 대해서 \(E[X] = Y'(1)\)가 성립하는 것을 알고 있으므로, \(Y(z)\)를 구해서 \(\bar{N}\)을 구해보자.
probability generating function \(Y(z)\)는 다음과 같다.
$$Y(z) = E[z^X] = \sum_{n=0}^{\infty} z^n P_n \quad \cdots (3)$$
식 \((2)\)의 양변에 \(z^n\)을 곱하고, \(n=1\)부터 \(n=\infty\)까지 식을 쓴 다음 양변을 더하면 다음의 식이 된다.
$$ \sum_{n=1}^{\infty} z^n (\lambda + \mu) P_n = \sum_{n=1}^{\infty}z^n(\mu P_{n+1} + \lambda \sum_{k=1}^{n} g_k P_{n-k})$$
각 \(\sum\)의 변수와 관계 없는 것들을 밖으로 빼서 정리하면 다음의 식이 된다.
$$ (\lambda + \mu) \sum_{n=1}^{\infty} z^n P_n = \mu \sum_{n=1}^{\infty}z^n P_{n+1} + \lambda \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} \quad \cdots (4)$$
편의상, 위 \((4)\)번 식을 다음과 같이 나누어서 정리하기로 하자.
$$ (\lambda + \mu) \sum_{n=1}^{\infty} z^n P_n \quad \cdots (5)$$
$$ \mu \sum_{n=1}^{\infty}z^n P_{n+1} \quad \cdots (6)$$
$$ \lambda \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} \quad \cdots (7)$$
그러면 다음이 성립한다.
$$ (5) = (6) + (7) $$
\((5)\)번 식 정리
$$ (\lambda + \mu) \sum_{n=1}^{\infty} z^n P_n \quad \cdots (5)$$
식 \((3)\)에서 다음을 알 수 있다.
$$ Y(z) = \sum_{n=0}^{\infty} z^n P_n = z^0 P_0 + \sum_{n=1}^{\infty} z^n P_n = P_0 + \sum_{n=1}^{\infty} z^n P_n $$
$$ \sum_{n=1}^{\infty} z^n P_n = Y(z) - P_0 \quad \cdots (8)$$
식 \((8)\)을 식 \((5)\)에 대입하면,
$$ (\lambda + \mu) \sum_{n=1}^{\infty} z^n P_n = (\lambda + \mu) (Y(z) - P_0) \quad \cdots (9)$$
\((6)\)번 식 정리
$$ \mu \sum_{n=1}^{\infty}z^n P_{n+1} \quad \cdots (6)$$
위 식에서 \(z\)의 지수와 \(P\)의 밑수가 달라서 불편하므로, 다음과 같이 같게 만들어준다.
$$ \mu \sum_{n=1}^{\infty}z^n P_{n+1} = \frac{\mu}{z} \sum_{n=1}^{\infty}z^{n+1} P_{n+1} = \frac{\mu}{z} \sum_{n=2}^{\infty}z^{n} P_{n} \quad \cdots (10)$$
식 \((3)\)에서 다음을 알 수 있다.
$$ Y(z) = \sum_{n=0}^{\infty} z^n P_n = z^0 P_0 + z^1 P_1 + \sum_{n=2}^{\infty} z^n P_n = P_0 + z P_1 + \sum_{n=2}^{\infty} z^n P_n $$
$$ \sum_{n=2}^{\infty} z^n P_n = Y(z) - P_0 - z P_1 \quad \cdots (11)$$
식 \((11)\)을 식 \((10)\)에 대입하면,
$$ \mu \sum_{n=1}^{\infty}z^n P_{n+1} = \frac{\mu}{z} \sum_{n=2}^{\infty}z^{n} P_{n} = \frac{\mu}{z} (Y(z) - P_0 - z P_1) \quad \cdots (12)$$
\((7)\)번 식 정리
$$ \lambda \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} \quad \cdots (7)$$
식 \((7)\)을 정리하기 위해 다음 부분을 떼어내서 생각해보자.
$$ z^n \sum_{k=1}^{n} g_k P_{n-k} \quad \cdots (12)$$
그러면 다음이 성립한다.
$$ (7) = \lambda \sum_{n=1}^{\infty} (12) \quad \cdots (13)$$
식 \((12)\)을 정리하기 위해서 다음과 같이 \(z\)를 분배해준다.
$$ z^n \sum_{k=1}^{n} g_k P_{n-k} = \sum_{k=1}^{n} z^k g_k z^{n-k} P_{n-k} \quad \cdots (14)$$
위 식을 보면, \(Y(z)\)와 random variable \(G\)의 probability generating function으로 정리할 수 있는 것처럼 보인다.
random variable \(G\)는 batch의 크기에 대한 variable이므로, \(G\)에 대한 probability generating function을 \(B(z)\)라고 하자.
$$B(z) = E[z^G] = \sum_{k=0}^{\infty} z^k g_k \quad \cdots (15)$$
편의를 위해서 식 \((7)\)에서 \(\lambda\)를 떼어낸 나머지 부분을 생각해보자.
$$ \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} \quad \cdots (16)$$
다음이 성립한다.
$$ (7) = \lambda (16) \quad \cdots (17)$$
이제 식 \((14)를 식 $(16)\)에 대입한다.
$$ \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} = \sum_{n=1}^{\infty} \sum_{k=1}^{n} z^k g_k z^{n-k} P_{n-k} \quad \cdots (18)$$
위 식을 풀어서 쓰면 다음 식들의 총합으로 나타낼 수 있다.
$$ \sum_{k=1}^{1} z^k g_k z^{1-k} P_{1-k} = z^1 g_1 z^0 P_0 $$
$$ \sum_{k=1}^{2} z^k g_k z^{2-k} P_{2-k} = z^1 g_1 z^1 P_1 + z^2 g_2 z^0 P_0 $$
$$ \sum_{k=1}^{3} z^k g_k z^{3-k} P_{3-k} = z^1 g_1 z^2 P_2 + z^2 g_2 z^1 P_1 + z^3 g_3 z^0 P_0 $$
$$ \sum_{k=1}^{4} z^k g_k z^{4-k} P_{4-k} = z^1 g_1 z^3 P_3 + z^2 g_2 z^2 P_2 + z^3 g_3 z^1 P_1 + z^4 g_4 z^0 P_0 $$
$$ \vdots $$
위 식들을 위아래로 합치면 식 \((18)\)이 되는데, 자세히 살펴보면 우변에서 다음을 알 수 있다.
$$ z^1 g_1 z^0 P_0 + z^1 g_1 z^1 P_1 + z^1 g_1 z^2 P_2 + z^1 g_1 z^3 P_3 + \cdots = z^1 g_1 \sum_{k=1}^{\infty} z^k P_1 = Z^1 g_1 Y(z)$$
$$ z^2 g_2 z^0 P_0 + z^2 g_2 z^1 P_1 + z^2 g_2 z^2 P_2 + z^2 g_2 z^3 P_3 + \cdots = z^2 g_2 \sum_{k=1}^{\infty} z^k P_1 = Z^2 g_2 Y(z)$$
$$ z^3 g_3 z^0 P_0 + z^3 g_3 z^1 P_1 + z^3 g_3 z^2 P_2 + z^3 g_3 z^3 P_3 + \cdots = z^3 g_3 \sum_{k=1}^{\infty} z^k P_1 = Z^3 g_3 Y(z)$$
$$ z^4 g_4 z^0 P_0 + z^4 g_4 z^1 P_1 + z^4 g_4 z^2 P_2 + z^4 g_4 z^3 P_3 + \cdots = z^4 g_4 \sum_{k=1}^{\infty} z^k P_1 = Z^4 g_4 Y(z)$$
$$ \vdots $$
위 식들을 모두 합치는 것은 더하는 순서만 바뀐 것이므로 식 \((18)\)과 같다. 식 \((15)\)를 이용하면 다음과 같다.
$$ \sum_{n=1}^{\infty} \sum_{k=1}^{n} z^k g_k z^{n-k} P_{n-k} = \sum_{n=1}^{\infty} Z^n g_n Y(z) = Y(z) = \sum_{n=1}^{\infty} Z^n g_n = Y(z) B(z) \quad \cdots (19)$$
이제 식 \((17)\)에 의해, 식 \((7)\)을 구할 수 있다.
$$ \lambda \sum_{n=1}^{\infty} z^n \sum_{k=1}^{n} g_k P_{n-k} = \lambda Y(z)B(z) \quad \cdots (20)$$
식 \((5)\), \((6)\), \((7)\) 종합하기
$$ (5) = (6) + (7) $$
이고, 식 \((9)\), \((12)\), \((20)\)에 의해,
$$ (\lambda + \mu) (Y(z) - P_0) = \frac{\mu}{z} (Y(z) - P_0 - z P_1) + \lambda Y(z)B(z) \quad \cdots (21)$$
